MICHELSON'S ERROR ©
3/2023
Steven Louis Grillo [slg@michelsonserror.info; slgrillo@gt.rr.com]
The first video presented here is a Primer for Michelson's Error. This Primer is intentionally provacative, driving as quickly as possible to the summary deductions that are important to this argument. Also, as a Primer, it is intended to be scanned quickly. { set your browser to playback at 1.25x.} This technique will allow a general absorption of the arc of the content, while revealing a detailed under-story that later works explore. Be advised to set the video viewer to full screen for clearest presentation.
The related videos and commentary that make up the corpus of this site follow a more sanquin deductive unfolding. Seen properly, this Primer is a functional abstract, though the second half of it jumps to a re-examination of a scenario that closley follows the theme that is the concern of Michelson's Error. Thank you...SLG
Primer for Michelson's Error
Given the aim here is to introduce Michelson's Error as directly as is possible, this next video is entitled, The Video Assay ~ Michelson's Error- part 2: Michelson's Error. It is a piece that has its own tailored introduction.
The Video Assay ~ Michelson's Error- part 1: Reviving Cartesian Concerns, for the sake of collective continuity, will be staged properly further down the site.
The Video Assay ~ Michelson's Error {2021: reviso:2023}is a rendition of The Fundamental Assay ~ The Last Piece {2018}. The Last Piece... is a written document supported mainly by graphics - but some animations do appear, especially in Appendix 3. The next segment, then, in an effort to be fully supportive, will feature Appendix 3; followed by Appendix 2.
So, as a global note, the top section of this site, through Appendix 2, will present the key elements that service this argument.
Appendix 3
Extension: The Four Analytical States of Concern; RE: Special Relativity Theory
Prologue: We will look closer at the four states of concern; those introduced elementally in the text proper [The Fundamental Assay {2018}]. This closer look will be supported by additional AVI files. Here, we will review the dynamical material under discussion more succinctly, and offer re-proofing notes. States 1 and 2 are tightly linked analytically; they form an important ground-figure scenario, illustrating in State 1 the classic interpretation, and its reciprocal in State 2. State 3 depicts a conditional to State 2; it helps maintain a mathematical purity to States 1 and 2, but a caveat must be noted. State 4 presents an analytically clear, but historically un-noted scenario. When properly interpreted, it undermines the Fitzgerald Contraction and defines how Einstein’s model relies on the imputation of inertia to a mass-less entity. We must find this a fatal oversight for the Special Theory of Relativity. Moreover, the gap intended to reveal the motion of Earth presumed to appear in the 1887 Michelson/Morley interferometer does appear in State 4, though not as originally anticipated. Thus, Einstein’s postulate that no experiment within an inertially balanced frame will reveal its motion is rendered moot. Motion in any frame is readily detectable when the tenets of State 4 are recognized and the proper technical procedures are brought to bear.
State 1 AVI
In State 1 we see the classic MMI prospectus, where the aether wind is pre-dominant. In this we see the wind as the figure and the device as the ground. As the light pulse leaves the source, it travels to the splitter; from the splitter to the far mirror; and from the far mirror back to the splitter. The distance from the splitter to the far mirror is L; the cycle there and back for the pulse is therefore 2L. However the pulse must deal with the flow of aether, and the analytical procedure for that circumstance is depicted by the V inscribed in the flow-by of the aether. Though the calculation emphasizes the time lapse, the V we see inscribed in the aether is a real spatial track the pulse must be seen to follow at c. And this track is longer than 2L; hence we say the cycle-time along 2L for a moving frame is slower than for a frame that is not moving - and also, it is cycling slower than for a frame moving not so fast as it. Though we use the term moving frame in the last sentence, State 1 requires us to remain mindful of the argument that the frame is ground, and the aether wind is responsible for the inherent vector the pulse encounters.
For the observer riding along with the source, the cycle along 2L is all he can substantiate as a scientific truth; he is in no way privy to the inherently inscribed path the pulse has traveled in the aether wind. If the cycle-time along 2L is his on-board standard measure of time, then he will never know that his cycle is lagging behind a cycle on a non-moving frame. This, then, is the root of time dilation and the normalcy of relative rest. When the frame/device is taken as ground, the aether wind taken as figure forces a un-noticeable vector on the pulse, where the observer on-board holds the pulse to follow the perpendicular path from source to splitter, and continue along the perpendicular to cycle through 2L (to the far mirror and back to splitter). It is an un-noticeable vector except for the sentient who can see, mathematically, the impact of the aether wind. State 1, then, is the preferred historical interpretation. See Sketches A and B
Note: For the mathematically inclined, it is clear that the aether wind in State 1 AVI is a very fast moving wind.
State 2 AVI
In State 2 AVI we hold the aether as ground and the frame/device as the moving figure. Though the State 2 AVI depicts a slower moving frame, all of the essential elements remain conserved. If the observer were astride the source, he would observe the un-noticed vector keeping the pulse on the perpendicular to him as the frame moves. But clearly the aether remains fixed as the frame and pulse move through it. The same math works as perfectly for State 2 as it does for State 1. But we take note of the pink dot that represents the illustrated start point of the pulse; it remains fixed in the aether as the source (and observer) continues on.
But now we ask a critical question: If the pulse remains on the perpendicular to the observer in State 2 – as to comport with State 1 - how and why? For the pulse to follow the V in State 2, it must carry inertia from the source [more importantly, through the splitter] – and this is not possible. Mass-less entities cannot carry inertia; and so, the un-noticed vector in State 1 and State 2 is impossible. Or is it?
State 3 AVI
State 3 AVI depicts State 2 AVI exactly. However, we allow ourselves a given: we presume the pulse to be deflected at the splitter by exactly the amount that would have it follow the inscribed V in the aether{ red-orange shadow }. It remains conclusive that a mass-less entity can be reflected or deflected along any path open to it, requiring nothing of the concept of inertia. A perfect deflection angle would allow the pulse to follow the inscribed V without violations of any sort. This mathematically solid argument helps certify the general conditions proffered in States 1 and 2. However, there is no known mechanism to physically produce this deflection in the MMI. Though the most analytically clean scenario, it fails in practice to help redeem States 1 and 2.
Keep in mind that States 1, 2 and 3 all exist here to help support the original Michelson/Morley analytical procedures, whereby the pulse, in following the perpendicular path, takes less time to return to the splitter than the pulse that was split off to follow the on-axis path. The proposed mismatch in the cycle-times was presumed to be due to Earth’s fundamental motion. When no mismatch (expected fringing) was found, it was left as a puzzle in physics until Fitzgerald produced a conjectural solution involving a shrinkage of L along the axis of motion – by just that amount that creates equal cycle-times for the independent pulses [on-axis and cross-axis]. However, there is no known mechanism to account for this shrinkage, except for the conjecture itself. But it stuck. And it was made all the sweeter when Einstein incorporated it into his own empirical observation. This observation held that the slowed cycle-times we witnessed in States 1,2 and 3, working in conjunction with the Fitzgerald shrinkage, suggested that such a frame is in a wholly unique expression of existence. The very physics of the frame were held in thrall to this slowed cycle, such that the given frame, in toto, had its own relationship to time – things age slower there. And beauty of beauties, the observer on-board would never know it – all would seem normal to him. And there would be no test he could ever perform that would reveal his inherent motion.
State 4 AVI
Dutifully, we turn to State 4 AVI, where we find the aether as ground and the moving frame as figure, and witness what nature would provide – an emission of a pulse that possess no inertia. The pulse is orphaned at the emission point and travels a path without heed to the moving away of the source and observer. It passes through the splitter at one point and returns to intercept the splitter at a different point. The implications here are profound. As the Accommodation Sequence in the text proper reveals, the pulses following this state of affairs sees the pulses emerging from the splitter perfectly in-phase, but with a gap between them owing to the motion of the frame.
Michelson and Morley expected the gap to be on the axis of motion, where State 4 reveals the gap to be on the cross-axis. There is no need to invoke the Fitzgerald shrinkage and, whereas the cycle-times do increase with velocity, the illusion of Relative Rest is broken because the gap can easily be garnered with the proper technical procedures – on any moving frame… Sentient beings should know they are moving through space when that is their future enterprise. State 4 clears the way.
The following AVI file depicts the Accommodation Sequence in close detail. We see the pulses in-phase and the gap indexed to the velocity of the frame. {The animation package at hand makes it difficult to synchronize all photon behaviors perfectly. Though stuttering, the phased depictions are in accord with the math algorithms constituting the Accommodation Sequence.}
Final comparison: Michelson/Morley vs Accommodation Sequence
On the left we see the output of the Accommodation Sequence, on the right we see the expectation of Michelson and Morley under a State 2 {moving frame} perspective, or to provide the correction they would need, a State 3 perspective {deflection at splitter}.
Appendix 2 is a necessary workbook that examines the behaviors of the rays as the device is rotated. Scanning these panels is helpful, but the Summary Graph that ends the sequence is most telling.
Appendix 2
Summary Graph
*******************************************************
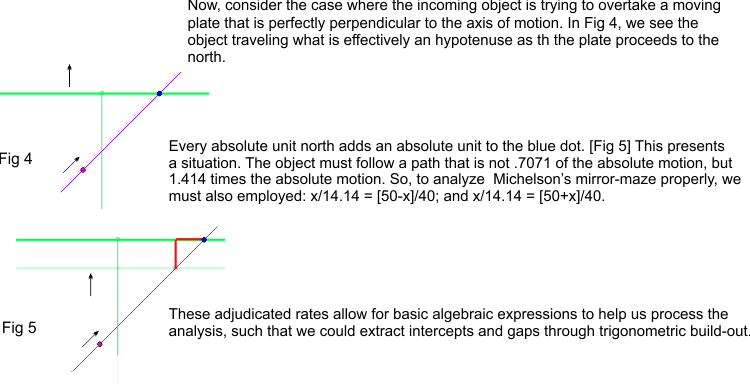
For general continuity, The Video Assay - parts 1 and 2 will be presented next as the originally intended matched pair .
3 Segments
December 2021 {reviso 8/22}
All fundamental derivatives and expansions copyrighted with all rights reserved by Steven Louis Grillo 2021
In 2020, I was able to complete 3 compositions that carry a tight relationship with one another. Early in the year, I finished a paper that isolated an error in A. A. Michelson's reasoning concerning the 1887 interferometer designed by him. It included graphics and animations to illustrate the assay of his work, and the implicit correction. {See Segment 3}
In support, mid-summer, I completed a brief which would bring the astute reader rather quickly through the arguments. {See Segment 2}
By late fall I had completed a 2-part video lecture that was a middle ground presentation of both papers. {See Segment 1}
Posted here, in reverse chronological order, are the the Videos as revised in Fall of 2021, the Brief and the Paper. For some, reading the Brief (Segment 2), and then reviewing the three appendices at the end of Segment 3, would be the rough equivalent of reviewing Segment 1.
Segment 1: Fall 2020 - Spring 2021 {reviso December 2021}
The Video Assay - Part 1: Bern Clock Redux {Reviving Cartesian Inherence}
Script for Bern Clock Redux: Bernclockreduxscript
To begin Episodes: Click white triangle in lower left of image
Episode 1/4
Episode 2/4
Episode3/4
Episode 4/4
The Video Assay - Part 2: Michelson's Error
Script for Michelson's Error: Michelson's error
To begin Episode: Click white triangle in lower left of image
**********************************************************************************************
This discussion has developed over many years. There have been larger papers, and smaller. Some drive with a very direct development; some elaborate with scenarios and vignettes. All told, they form what I have come to call, The Fundamental Assay. What follows is a brief that was intended to elaborate and parse a larger paper, produced in late 2018 and early 2019. As Segment 1 presented mainly video lectures, Segment 2 will present a textual document, with supporting graphics.
Segment 2: Summer 2020
Brief Concerning A. A. Michelson’s 1887 Error in Applied Mathematics:
Improper Foundation with Regard to Inertia© 2020 All rights reserved.
Steven Louis Grillo
October 2020
*******************
There came a day certain in June of 2018 when a mathematical solution presented itself as the final piece of a long- standing inquiry. With regard to today’s advanced mathematics, it is a very tame bit of work, but the logic problem to which it speaks is apt to be very, very telling. A larger paper has been written in 2018 to satisfy this solution’s intrigues. [see The Fundamental Assay, (www.michelsonserror.info)] Here, this brief will be a reduction to key elements such that the seminal idea can be circulated in its tidiest fashion. {This observer is operating as a natural philosopher, and so, simple vignettes and schemas will appear, as necessary.}
The focus of our attention, then, are the elements (taken as a composite) which enable Einstein’s construction of Relative Rest. Of course, the well-accepted model of Special Relativity is, in most ways, represented by Relative Rest, but it seems true to this observer that ragged intersections with other regimes of logic have attended it since its inception. To wit: it seems odd that a creature, as sentient as is a human being, be so lost in a Relative Rest frame that he cannot surmise his motion through space as he progresses from one star to the next. This seems a very ragged concordance with reason. After several decades of reflection, this observer designed on paper (never built or ran) a device that would allow an observer subsumed within a rest frame a to verify and index his motion {velocity} through space against light’s velocity through space. Should this test /device ever be executed, it will reveal that violations of the tenets of Relative Rest have been available since 1992. However, even as the test was designed specifically to violate the tenets of Relative Rest, and thereby bring new scrutiny to the larger model, it was clear that the essential flaw in the model was not isolated by the test, itself, i.e., the new scrutiny would hopefully find it – a task presumably larger than this observer’s ken.
And so, the task since the early 1990’s was to fortify the value of this {in the head} design by building a clearer and clearer deductive path - through numerous vignettes and scenarios - that would validate the presumed functioning of the test, so that properly skeptical academics might turn to physically produce its surprising outcome. As things sometimes go, the elemental work with the vignettes left this observer a stone’s throw away from the essential flaw. Alert: the essential flaw is not within the concordance of logic that builds Special Relativity – Einstein’s model is acceptably correct, if all the underlying pieces are correct. They are not.
Einstein’s thinking merged with that of the empirical avant-garde that laid the foundations of the industrial revolution starting – as you like it – circa, 1885. Indeed, it can be argued that Einstein was the most avant-garde. What did he do? His model of Special Relativity promulgated the view that Cartesian space had no value in proper scientific assessments. A scientist’s laboratory is his kingdom - and his only kingdom. This was one of Einstein’s prime tenets; i.e., what happens to an observer’s lab equipment is the only proper data to be collected. In classical Cartesian times it was possible to start a trial in space at point A and end the trial in space at point B, holding point A to be the origin and B the terminus – meaning, absolute beginning and absolute end. No such absolutes can be maintained under Special Relativity; there is no absolute rest point – in fact, then, there is no absolute motion. All frames relate to one another through purely relative means – each being a conditional rest point, the other in motion relative to him. And this means every frame in uniform motion (a non-inertial frame) can hold itself at Relative Rest, with all other things in the universe in motion relative to his rest-ness. If all of this seems to smack more of circularity than of sophisticated empiricism, welcome to this observer’s concern with Relative Rest.
Now, it might occur to you that Einstein’s proposition, i.e., Special Relativity, might be a very hard sell in the market-place of academics, due its purely esoteric reasoning; it would be (and was) - save one crucial physical fact - the outcome of the 1887 interferometer experiment by Michelson and Morley. We can say more broadly that their experiment marked the beginning of the end of the classical Cartesian era, and the beginning of the beginning of the modern relativistic era. We can also say, more specifically, that the reported outcome of their 1887 experiment was an excellent physical manifestation of Einstein’s 1905 model. But we can also say, though the 1887 experiment is a key-root to Special Relativity/Relative Rest, it is within said experiment that we will find an error that disassociates it.
The aim of the following pages will be to parse the attendant logic models that are incumbent upon the 1887 design. Mainly, we will reveal how inertial and non-inertial components were improperly fused as Michelson applied the presumably correct mathematics to the design. We will begin with a simple vignette….
We begin with an elongated box, a square tunnel if you like, 10 feet long {open end to open end}, and 3 feet square. At the mid-point of the long side, we attach a tennis-ball cannon. [See Sketch1] To begin, we seal the ends and create an effective vacuum. When the cannon is fired, we observe the tennis ball to cross the empty box and re-coil from the far wall to return to the point it exited the cannon. This we see is very much a straight line path there and back again, ignoring any dropping due gravity.
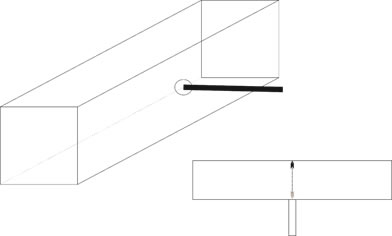Sketch 1
We now alter the vacuum to accommodate a very low pressure flow. We attach a hose to one end. The hose will inject a very low density smoke to flow from one end and exit the other. Now firing the tennis ball we observe it to follow, due the very low density of the smoke versus its high inertia, for all physical purposes, another straight across and back again path. However, given a meaning flow to the smoke, an additional path will be evident in respect to it. There will be a path of disturbed smoke that will look, at the return of the ball to the cannon, like a V, and it will remain suspended thusly until the body of smoke that contains it exits the box. [See Sketch 2]
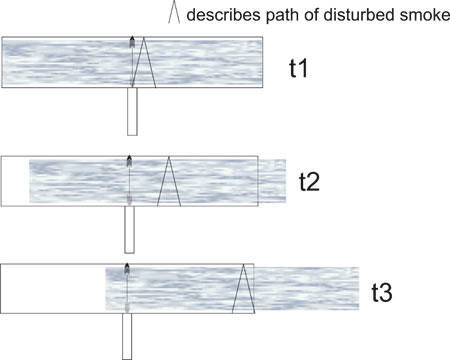Sketch 2
At the highest level of complete analytical precision, we can say the ball experienced resistance due the smoke particles it encountered and was deflected a slight bit down range, such that it did not hit the cannon barrel dead center. Most importantly, we could say the time of its cycle, there and back, would be longer than that of the no-smoke trial. What we are looking at here is an argument that diverges into two main paths. Taking note that the tennis ball has the same velocity and inertia each time it leaves the cannon, we can see one path where the smoke becomes denser and denser forcing the ball to slow as the density increases , thereby creating a wider V, as it takes longer and longer for the ball to get to the far wall and back.
And another path where the smoke becomes less and less dense allowing the ball’s cycle time to approach, by increments, the original cycle time of the ball in the vacuum. And as the smoke gets thinner and thinner yet, the enclosed volume approaches the original vacuum itself. With this extremely sparse smoke, we can increase the velocity of the particles significantly without perturbing the path of the ball in any appreciable way. Now we can see the V getting extremely wide as the virtual smoke flies past an object with too much inertia to notice their passing. The point of this exercise is to point out an exotic circumstance: if a single smoke particle enters the box at 50 times the speed of light and never touches the ball, there would still be a virtual mathematical V that describes their relationship. And that relationship informs the design of the 1887 Michelson/Morley interferometer, albeit with more mundane terrestrial values; namely, the speed of light and the velocity of Earth. And, as mentioned earlier, this is where the trouble gets started.
Now there are some that will say we ended the last vignette with a nonce proposition. The ball did not perturb anything to create a V; so, really, that observation is essentially correct. But, stepping back to 1887, how do you perturb something as nebulous as luminiferous aether? That question is very likely too esoteric for us to answer, but nonetheless, Michelson and Morley were relying on just some such interplay to inform their test. If we are allowed to return to 1887 and examine very carefully the parameters set before them, something that should be very interesting to relativists just floats to the surface.
By 1887, it had been fairly well established that light had a finite velocity and some (including Maxwell) had earlier seemed inclined towards the idea that it traveled through a luminiferous aether. It also seems that Maxwell, himself, had suggested that it could be determined optically. Either way, A. Michelson using the basic paradigms of his day designed, with expertise borrowed from E. Morley, what in history is termed the 1887 Michelson/Morley experiment. Certainly, the velocity of Earth on its orbit was known to be 30 km/sec. Clearly, light had a finite velocity of 300,00 km/sec. If light were to be found traveling in the same direction as the Earth, then the one should subtract from the other and an indexed velocity between the two should be obtained. So obvious was the idea, why even do the test? Michelson had actually tried in 1881 to produce this indexed result but concluded his test equipment was too crude to deliver the proper answer. But still, why not test for the sake of improving the precision of the components. And so, in 1887, the chance came for a more rigorous build-out and the seemingly certain {expected} result, again, did not materialize. By the data from his test, one could conclude that Earth was not moving. No one considered that a possibility, so all of light-oriented physics was dumbfounded for a while. Then, in 1889, G. Fitzgerald offered a solution. Maybe physical things shrink in the direction of their motion by that amount that erases the Michelson expectation. Note that this is a very Cartesian argument; Fitzgerald meant motion as in moving from point to point through the firmament of space, regardless on what medium light moved through it.
Now for some details: Michelson’s main premise was that a beam of light could be split into two other rays by passing that beam through a half-silvered glass plate, a porous mirror, if you like. For his time, not a technically difficult feat. The more technical trick would be to divert the rays at 90 degrees to one another by setting the porous mirror at 45 degrees to the beam source. Again, not supremely difficult. But now these split beams must go out, be reflected by fully reflecting mirrors, and then return to the point on the glass plate that hosted the splitting. [see Sketch A] Doable, but real precision is required because the test relies on examining the phase relationships of the waveforms, themselves, as they proceed to the target – and these waveforms, or more accurately, these wavelengths are tiny. So the length from split point to each reflecting mirror had the be exactly the same. And that was an appreciable task; so much so, that one of the reflecting mirrors had to be made movable. But again, that final bit of precision could be mastered. Importantly, we must now look at the math to see what Fitzgerald did - when all of this precision failed.
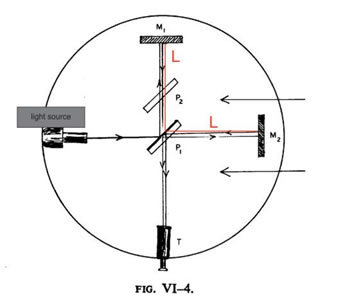Sketch A
With Earth moving at a given velocity and light moving at a given velocity, taken against a distance L , we have two separate calculations to make. When executed, these calculations reveal that one ray should return to the split point slightly later than the other. For P1 and M1, the math that calculates the round trip (total cycle) of the beam (ray1) looks like this: 2L/V/ sqrt (1-v~2/V~2). For P1 and M2 (ray2), the math looks like this: 2L/V/ 1- v~2/V~2. [ V= light-speed; v= Earth-speed] Here, the first expression computes the shortest cycle. Assuming that ray1 is reflected at 90 degrees at the time of the splitting, it will travel to M1. Upon reflection at M1, it will return to P1, where it passes through the glass plate to T. In conjunction with that activity, ray2 passes straight through the glass plate at the splitting; it will travel to M2. Upon reflection at M2, it will return to P1 and take its turn to be reflected 90 degrees toward T. [See Sketch Bz] Now many of these split pairs will not perform as the ideal model presumes, but continuous pumping of beams from the source, insures success.
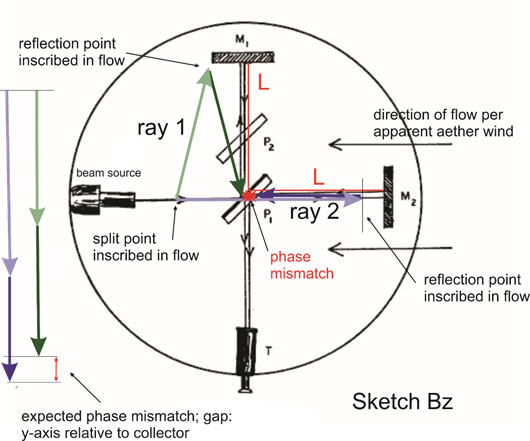Sketch Bz
Of course, we see ray1 returns to P1 before ray2 does, and this gap is due totally to the real motion of Earth at a given speed. However, even with this analytically valid and very precise arrangement of gear, the gap did not appear. Fitzgerald saw that by physically shortening the path taken by ray2 by a value equal to sqrt(1-v~2/V~2), the two rays would then be found to have equal cycle times, and what was observed {no gap} would be in accord with the old mathematical procedures taken against a new empirical paradigm. It simply requires the miraculous removal of a bit of one of the physical legs – due to the device’s motion though space.
To begin the critique that is the conceit of this brief, we start with the global assay that Michelson and Morley faced. Knowing that Earth had an orbital velocity of 30 km/sec, the only way to set a control {at rest} scenario would be to set the system in motion at 30km/sec against the orbital motion, and include the rotational component. So, just as a rough number, they would have to have the system leave New York, heading to Los Angles, at 38.5 km/sec. In 1887 the only thing that might could achieve 38.5 km/sec would have been a mortar shell – so, forget a control. Their only option was to reciprocate the whole logic and treat the motion of Earth as zero, and have the luminiferous aether flow at 38.5 km/sec through the system. It was already presumed in many circles that the luminiferous aether was a fixed unmoving matrix in the firmament. So an apparent aether wind of 38.5km/sec became a component in their system. Sketch Bz shows us the expected outcome of a trial.
What we see from the given mathematics is that these expressions compute total time cycles for a fast moving entity as it inter-operates within a frame of given length, which is, itself, moving as some slower pace; very simple algebraics. But in this reciprocated scenario the time cycles are more about forces interacting. For ray2, it is traveling against a flow which slows it down with respect to the reference frame. Leg1 {light blue arrow} takes the longest time of all the other legs because it faces most directly the force of the flow. Leg 2 {dark blue arrow} takes the shortest time of all the other legs because it has the full benefit of the flow, acting, as it were, as a tailwind.
So we see for ray 2, the beam leave P1 at 300,000 km/sec to fight a 38.5 km/sec headwind. When this resultant vector is taken against the Cartesian length L, it will take a certain time to make it to M2; and upon reflection at M2, it will be escorted back to P1 by a 38.5 km/sec tailwind. Taken strictly against the Cartesian L of the fixed device, the ray has traveled slower than the accepted speed of light on its way to M2, and faster than the accepted speed of light on its return to P1. But it remains true that the cycle time for this behavior is correctly computed by Michelson’s original math.
Ray1, under this vector scenario, is shown to be working cross-currently to the aether wind on its trip to M1. The key interpretation here is that it leaves P1 and travels L to M1 and returns to P1 always on the perpendicular that this schema insinuates; it is not blown down-wind by the 38.5 km/sec flow. Again, a simple resultant vector will account for this un-deviated path, and again Michelson’s original math will compute the correct cycle time. But, of course, ray1, not having the full expression of the flow to defeat, will trace L in less total time than ray2.
So, for the first hard check this document promises: It is perhaps a curious question to ask, but what happens to a light beam when it encounters a gust of aether head-on, or what happens when it is blasted from the rear by such a gust. Given that the aether was considered fixed in the firmament, these are moot questions to be sure; but when we see the beam attempt to cross a flow of aether, as in ray1, and remain true to a given heading, then we must begin to wonder - how is this force-like entity acting mass-like? If this seems like an unfit question at this point, let’s parse a bit further.
Let’s call the apparent aether wind scenario {above}, State 1 [see Sketch Bz]. We can say it is the state that has been delivered to us historically, because, well, they impute an apparent aether wind in their elemental assay. For State 2 [see Sketch Cz] we re-set their original assay by removing the aether wind. We will now explore moving the device {frame} through a fixed aetheric integument. {Note: we can still say there is an apparent aether wind relative to the moving system, but here we emphasize the fact that the frame has the only motion.}
Sketch Cz
If we again begin with ray2, we can see perfectly valid conditions on all points. As the ray leaves P1, it will travel at its accepted speed through the aether. However, the L bounded by P1 and M2 is now also moving through the aether; is receding at 38.5 km/sec through the aether as the ray approaches it at 300,000 km/sec – its accepted aetheric speed. Upon reflection at M2, the ray will return to P1 traveling through the aether at 300,000 km/sec as P1 approaches it, traveling through the aether at 38.5 km/sec. And, again, Michelson’s math will compute the cycle time correctly. But here we make a critical observation, P1 is not at the same Cartesian point in space that hosted the splitting - P1 has moved; as did the whole frame with it. [Special note: for Einstein’s model, this observation means we are reckoning outside of the lab, and, therefore, this is unacceptable reckoning. {P1 is the only source to reckon by in Relative Rest.}]
For ray1, the ray will leave the split point, travel to M1 and return to the new P1 position, presumably, in perpendicular alignment with P1 as P1 moved. And again Michelson’s math will correctly calculate the cycle time of this behavior. And, of course, ray1 returns to P1 before ray2 does. And here, our argument must christen itself – the beam {ray1} is acting wholly mass-like to accomplish this behavior. {Perhaps by reducing the beam to a single photon that is following this path makes it clearer in the mind.} State 2 has shown us a perfectly valid presentation for ray2, but shakes us as we must accept that ray1 is following a path only a mass object possessing inertia could.
State 3 [see Sketch Dz] offers us a fix to the dilemma in State 2. For ray1 to accomplish this mass-like behavior, it simply needs to be deflected by that perfect angle to compensate for the velocity of the frame and the distance to M1. Mathematically simple, and this solution jumps cleanly over any mass problems in the behavior, a mass-less entity can be deflected into a fixed aether at any angle. This deflection will allow the photon to remain on the perpendicular to the split point on P1 as P1 moves through space, acting, as it were, like an entity that will move straight away and then return directly to P1 – imitating a rest scenario. Of course, for this general solution, there is no mechanism to induce this deflection at the split point.
Sketch Dz
State 4 allows us to illustrate these essential behaviors, but holding as key components - a moving device, a fixed aether and a beam/photon obeying inertia rules for a mass-less entity.
Before we turn to the details of State 4, it would be helpful to review Michelson’s essential guide-ons.
Michelson needed an estimate of the gap that should appear in this process. The known orbital velocity of Earth (30km/sec) seemed the largest reliable component; and so, a gap based on that orbital velocity was computed to be 5 ten-millionths of a percent, taken as comparative arrival times of the rays. This gap helped inform the choice of wavelength that should be used – a wavelength that was too long would produce rays that would lie too closely together at such a tiny separation to produce effective fringing. The wavelength that was chosen had a vibrational period that was longer than the gap such that only 2.5 percent of it presented to the gap. This seemed to be enough injection to produce workable fringes. What we see by Michelson’s construction is that the frame would not move very far in the time it took light to cycle through the mirrors. State 4 [see Sketch CzB] will introduce alternate computational elements.
In the discussion of States 1 -3 we were using 38.5 km/sec as a general estimate of velocity incumbent on the processes in the device so to suggest that more than the orbital component might should be considered. We were adding a bit to reflect the rotational component as well. For comparative clarity we will use Michelson/s 30km/sec for numerical computations.
In State 4 we concentrate on what a moving frame through a fixed aether may offer. Chiefly, we will emphasize that the mass-less entities should behave as mass-less entities are thought to behave, but that will require noting origins in Cartesian space – a concept lost by the relativistic overlay. So simply reviewing Sketch Cz [See Sketch CzA] – though nowhere close to scale - we still see that the distance traveled by P1 creates a gap larger than Michelson’s assessment. And numerically we will see this is true.
Sketch CzA
But what looms large in State 4 is the observation that, as the rays/photons should behave as mass-less entities upon reflection, Q3 and Q4, representing ray1, remain co-incident on the perpendicular to the split point inscribed in space, and not the moving plate. So, parsing carefully, we see the rays/photon leave the actual split point on P1and move toward M1 with no downrange component of inertia. With these gaps exaggerated in the given graphics, we should understand that M1, with a width of 50, cm would be easily intercepted by that cross-current beam, given Earth’s orbital velocity. Noting that these two rays, after the split, will travel at c along their respective paths, and keeping in mind that the calculations for the on-axis math are correct, when the ray returning from M2 intercepts P1, the ray from M1 will have traveled the same distance {ray1= ray2} and, therefore, will be slightly beyond the split point inscribed in space. [See CzB] So then, when the on-axis ray is reflected toward the target (collector) it will, in fact, be lagging behind the cross-current ray, thereby, creating the phase discrepancy presumed by Michelson. We can say this gap lies on the y-axis relative to the collector. By this reckoning, it is larger than Michelson’s gap by a physical factor of 2, so, by extension, 5 percent of the wave period is presented to the gap. But more remarkably, noting the red lines, there is an additional gap in the offing.
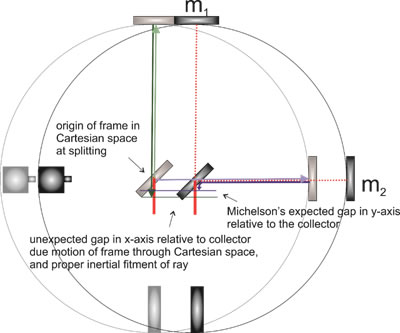Sketch CzB
This gap lies on the X-axis relative to the collector. What has historically destroyed this gap is the tuning of the mirrors into one coincident image on the screen, in an attempt to search for the only gap (on the y-axis) that is ever presumed to exist by general design – a design that dysfunctionally imputes inertia to a mass-less entity. The un-expected gap’s width, in this case, is the distance the plate has moved until the ray returning from M2 intercepts P1. With the terrestrial components at hand this is equal to .6 millimeters. So by inference, when the two images are brought to approximately half a millimeter apart, they are indicating a 90 degree angle to the tuning mirrors has been achieved. Of course, key astronomical orientation is to be respected.
So, thus far, State 4 has shown us important details; continuing, we find other novelties. So this device is to be rotated to capture its probative data. It was originally floated in mercury to provide a nearly frictionless movement. Though rotation through a full 360 degrees would provide a robust data set, key elements appear in 90 degrees of rotation. For the above analysis we have shown the source positioned on the 270 degree point with the direction of movement west to east, i.e., the beam source lies on the axis of motion. If we rotate the source to the 315 degree point, we see the gaps fall to zero. When we rotate to 360/0 degrees we see the beam source perpendicular to the axis of motion. And a new, more surprising, tale begins.
Again, ray1 at P1 is reflected and heads to a now receding M1; its complement, ray2, passes through at P1 and is not affected by any motion the device possesses. Ray1 at M1 is reflected slightly after ray2 is reflected at M2. When ray1 from M1 intercepts the plate at it new spatial location, ray2 from M2 has already passed through the spatial origin of the split. [See Sketch CzC]
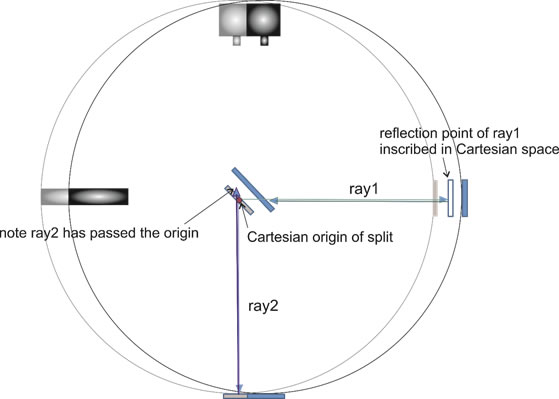Sketch CzC
Just at this instant, an accommodation sequence begins. The ray from M1 will pass through the spatial origin just as the ray from M2 intercepts the continuously receding plate {by definition the system is moving right-ward, but the angle of the plate creates an apparent recession to a line fixed in space perpendicular to its motion}; at the instant of its reflection towards the screen, we find both rays perfectly in-phase but separated by the same .6 millimeters as earlier - plus the compensating tiny fraction the plate continued to create until final exit; i.e., the gap is wider by the amount that represents Michelson’s y-component we found in the trial with the source on-axis. [See CzD]
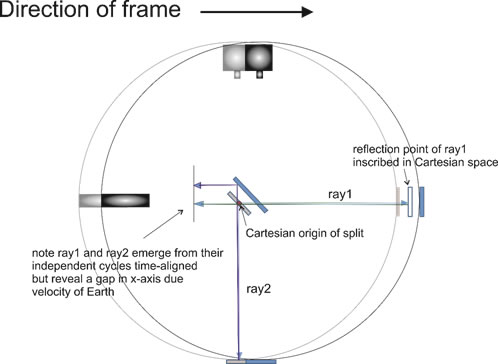Sketch CzD
When the rays have run their cycles through the device, they exit in-phase (from a cycle-time or distance traveled perspective), but with a gap between them in the x-axis, owing to the specific velocity of the frame.
Consider the 8 major way-points on a compass: if there is motion of this device to the North, then, when the source is at ENE, E, ESE, WSW, W and WNW, it can never produce any of the phase mismatch in the y-axis (relative to collector) that captured Michelson’s focus. Of these 6 way-points, 4 produce no gap and 2 produce a gap in only the x-axis relative to the collector. When the source is at the N and S points, some distinct mismatch in the y-axis occurs, in conjunction with the unexpected gap on the x-axis. But with the mirrors functionally tuned to the essential destruction of the unexpected gap, it is hard to say what to expect of this disfiguring triangulation except a muted overall response.
Further, reckoning with the rays as non-inertial entities as we have in State 4, a general over-arching behavior presents itself as the device is rotated: there would be a natural min-max deviation from the perfect end-points of the cross-current axis [points of tangency on east – west axis relative to the Northerly motion]. Indeed the rays would never fall on these exact points; they would always fall below them, and drift more southerly and then back more northerly through the rotation. But again, with these rays normally tuned to erase the unappreciated gap, this behavior would likely look as if the apparition, in in toto, was ever so slightly drifting a bit one way and then reversing, wavering back and forth. [See Appendix 2 TFA]
In a way, this brief has been an elaborate abstract for the treatise below: The Fundamental Assay – the Final Piece, 2018. In that document are animations which help support the graphical figures presented in this brief. Our conclusion in this brief draws our attention to Michelson’s analytic applications taken as math. The on-axis expression would succeed as it should because it is valid for the case of two entities moving at different velocities; where one is a given length moving at one velocity, and the other, at its velocity, is cycling within it. The related expression ascribed to the cross-axis, however, succeeds only in an inertial case. We are illustrating that what lies before us, considering the 1887 device and experiment, is a non-inertial case for the mass-less entities involved. To correct Michelson’s analytic application we simply apply a single algebraic computation, and then parse what must be true in a non-inertial circumstance as the elements evolve. Noted earlier as valid, we calculate the on-axis cycle time using 2L/c/1-fv~2/c~2; where fv is the frame’s velocity and c is light speed - then consider the spatial implications of a non-inertial path for the complimentary ray. What results from this inertia-aligned parsing is a) the observation that the historically expected gap {due orbital velocity of Earth} does appear but primarily in an unexpected dimension, and b) the rays emerge time aligned [in-phase] in 6 of the 8 major way-points, to continue abreast through space. This leaves only two way-points to reveal the Michelson y-axis gap. This observer holds that these two gaps can, and will be isolated. This satisfyingly reduces the Fitzgerald Contraction to so much futzing, and its empirical overlays {Lorentz transform, Special Relativity}, though coherent constructions in logic based on such a contraction, scuttle at launch as tools for modeling reality. We simply need to remove tunable mirrors to see what this class of interferometery actually holds.
We conclude referencing Appendix 0, which develops a numerical exercise to illustrate the accommodation sequence, and invite the reader to move, thereafter, directly to Appendix 1 at the end of the following paper for notes on adjusting the standard Michelson interferometer, and then, to Appendix 3 for animations that support the earlier insights mentioned in States 1-4.
Steven Louis Grillo 10/4/2020
Appendix 0
Forward: Personal notes on Historical Development
On June 15, 2018, I woke to turn to my scratch pad, and within a 2 hour span I had resolved an issue that had been with me for decades. To jump way ahead, I had found the mathematical error that had eventually given rise to Special Relativity. Suffice it to say that for all those aforementioned decades, I knew something was wrong with the model built by A. Einstein, commonly referred to as the Special Relativity Theory. Even though the general concordance with some factotums provides the model with some strength, the stretching of space-time seems, at times, like the stretching of wool across our eyes. By the end of this document you will come to see a few the issues as I see them, and I will entertain you with my solution, leaving you to consider its plausibility. Science will out, either way.
Einstein illustrated his model with vignettes. Famously, he once described time dilation thusly: [paraphrasing] …you know how, when you are sitting on a fence with a pretty girl, time passes all too quickly, and when you place you hand on a hot stove, time passes all to slowly,, that is relativity… And so began my intrigues and deliberations [1975-1985]; I mentally built scenario after scenario, exercising what I could to grow fluent in the model, but all too often what started well, ended poorly. I was either incorrigibly dense, or I was on to something. By the end of the next decade [1985-1995], I had worked out a bit of math, but more importantly, I had finished a one hundred page treatise that explored my failures to comprehend. The key aspect of that paper is that I offered up a design for a test that would catch Special relativity out of its depth. Namely, prove that, within an inertially balanced frame, one could extract proof of one’s uniform motion, even use the data to index that motion (velocity) to light’s velocity. [The very aim of the Michelson/ Morley interferometer in 1887] To this day, this test has not been done, though no exotic equipment is required, save an atomic clock or two.
So I must make clear that this test was only a shot across the bough, so to speak. It would almost certainly produce the results the intrinsic thinking predicted, and that would leave science (and scientists) a bit slack jawed, but it was clear to me this would only reveal that the model was broken, not how. Of course, throwing such a monkey wrench into the theoretical mix, should be thought of as quite a life’s accomplishment. I could only surmise that the final solution would require equipment to which I would never have access. The next decade [1995-2005] produced various related articles, and yet another treatise, looking, as it were, at both the analytical and historical roots of the SRT model. In that treatise, there are many graphics, along with some telling animations. Between 2005 and 2015, the exploration proceeded with further looks at improved vignettes, and elemental write-ups that would serve as the backbone to a book when the time came. So beginning in 2015 I began to gestate on what a book should look like; more explicitly, what would a publisher need to see to green-light a contract. And so the classic chicken and egg problem: without a scholarly thumbs up, these arguments are the plinkings of a music box swept up in a tornado; without a full book-length description the plinkings cannot be isolated for the scholars to consider. And so began a growing consternation - the keystone of the book would be the test designed way back in 1992 – the rest would be extrapolations from my deliberations that might point the way to a final solution, but all of this is just so much mental cabbage without B helping A or A helping B!
So I began to prepare a presentation for the scholars. This would require me to take a global view of all my efforts and reduce them to a series of key arguments, and that took all of 2016 and most of 2017. This left me with a pile of things well spoken to and a pile of things that needed answers. No argument is flawless, but I began to attend to the hard questions left to be resolved. Weeks went by; months went by; and finally I woke on June 15, 2018 thinking that my thinking could reach to the end of one of the hard one’s - within hours, my scratch pad said it could.
By the end of 2018 I had finished the essential work that follows here. The June insight produced more than just a stitched off end to help a book deal, or positive scholarly appraisal – it solved the problem rather entirely. 2019 passed quickly as I spent time improving the animations I could render. The turn of 2020 presented an opportunity to have the work pass before some eyes at NASA. But covi-19 put most such agencies in turmoil. The Fundamental Assay has been polished along the way. Here we will present the 2018 work in its latest form as an historical marker, though the 2020 brief {above}: Brief Concerning A. A. Michelson’s 1887 Error… covers the material more succinctly – and adds a curious detail that an additional two years of work would supply.
Segment 3: Fall 2019 - Spring 2020
The Fundamental Assay
The Last Piece
Steven Louis Grillo
07/09/2018
*************************
The abstract here is simple: We will examine the original 1887 Michelson /Morley experiment and parse carefully the elemental states of logic presented. We will further integrate the importance of inertial and non-inertial behaviors with respect to the given components. We will also see how Einstein’s model masks Cartesian underpinnings that should no longer be ignored.
***********************
Over the course of some thirty years, the focus of the work here has been a global assay of Einstein’s model of Special Relativity. Many is the number of physics and engineering students that has begrudgingly bitten the bullet to accept what was presented, feeling all the while something was amiss. The model is beautiful in its way, but still… Perhaps the following will lend a hand to their suspicions.
We can say this assay has its beginnings in the classic way of all divergence; an attempt was made to comprehend the rigors of the model. After numerous quizzical moments dissolved into a rudderless fugue, there came an aha! By itself, not much of an aha!, but once the lightning arc connected two regimes of logic, the game was afoot. A thirty year game, but nonetheless…
The beginning, of course, was in Einstein’s head, and his many reflections on the nature of light and space, but those thoughts eventually collided with a puzzle produced in 1887 by a pair of researchers named Albert A. Michelson and Edward W. Morley. They designed what all then-current scholars thought was an ingenious test in an attempt to capture telling information about how light integrated with the motion of Earth. Indeed, it was considered almost an unnecessary test, so good was the predictive nature of the design - akin to dropping a ball from shoulder height to the ground to demonstrate gravity. So design in hand and device built, the inevitable flipping of the switch came to pass. And what a shock, none of the expected behaviors occurred in the device. It was what can easily be described as a spectacular fail in physics, leaving in its wake a REAL puzzle to attend.
Albert Einstein was 8 years old in 1887 when this puzzle developed, and his model/solution was presented in 1905 when he was 26. Meanwhile, there was movement on the problem. In 1889, G. F. Fitzgerald put forward a working solution that tidied things up in a general way. He proposed that an object/frame shrank in the direction of its travel. An arrow shot through space became shortened when compared to its identical companion still in the quiver. Notice this is a one dimensional solution – the arrow flying through space, unencumbered by any other component, is shrinking along only one of its 3 dimensions as it passes through the realm of static space. Fitzgerald does this by re-engineering a two-dimensional math problem. We can say here, it works – but we will need to look at the classic set-up of the Michelson/Morley interferometer to see the proper elements unfold. Later, we will critique the set-up.
As mentioned earlier, the aim of the Michelson/Morley interferometer was to show, actually calculate, the velocity of Earth through space. They relied on a well-understood analytical construction for their design. Their device would be riding on the skin of Earth at one velocity (the x to be solved for) and they would bounce light at its velocity around in the device. The thinking in that moment was that when the dust settled the light should be diverted in such a way that the one beam becomes two parts, and the two parts end up out of phase due the velocity of Earth. This phase difference could be measured, and the velocity of Earth derived from that…not really that complicated. All they were going to do is send a beam of light through a plate of glass that was lightly-enough silvered such that some of the beam would pass straight through the plate and some of the beam would be reflected at a 90 degree angle to the other. Each part of the split beam would go the same distance from the split-point and be reflected back the way it came. Again simple enough, but the actual path of each part was subject to its own math treatment. Taken together, one part would take longer for its total journey than the other. That final gap due to Earth’s velocity.
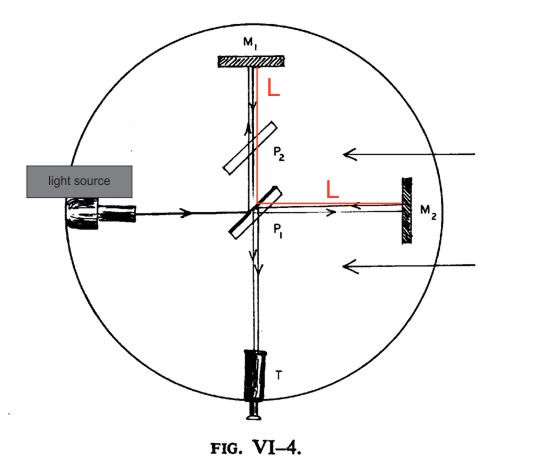SketchA
The diagram above was clipped from a book by George Gamow*.
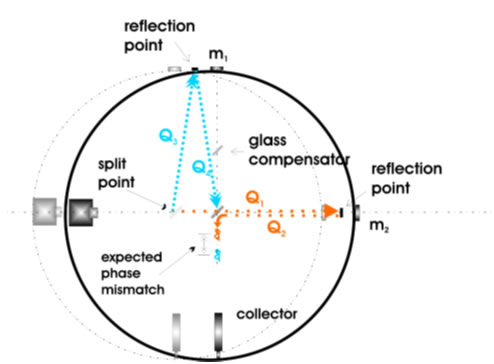
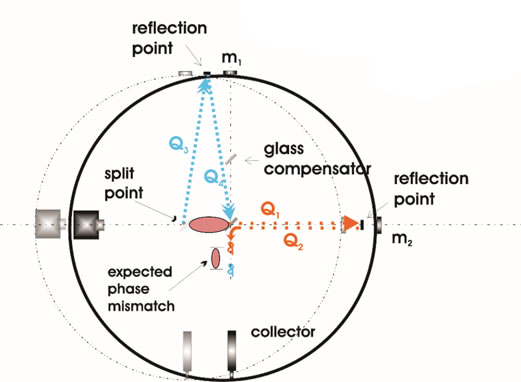
Sketch A shows the simple design of the interferometer, which relies more on a precision build than a complex design. Note the two arrows coming in from the right; they represent the apparent flow of aether that Earth was presumed to move through. So the given direction of travel here is for the device to be moving to the right, inherently, the flow is taken to be moving to the left. The Fitzgerald contraction (as the shrinkage came to be known) is happening between the light source and M2; or more precisely for the math, P1 and M2 . [P2 is an extra plate added to make sure each split of the beam travels through the same amount of glass, given the slivering is on the surface of P1 nearest the source. Given this set-up, the global analysis must take into account that the beams, once split, must travel – one, into the flow and back, and the other, across the flow and back. Each of these require their own math treatment, and they are similar but not the same. The assumptions that regulated the original test had no consideration of contraction, so this how the math was invoked to work: from P1 to M2 back to P1 (distance = 2L) we get 2L/c/1- v2/c2; and from P1 to M1 back to P1 (also distance =2L) we get 2L/c/ sqrt(1- v2/c2).
These expressions are technically calculating the time each split of the beam must take to go and then return to the splitter, P1 , due, in this case, the wind they must encounter - a simple class of vector. The beams then go on to emerge from the system – presumably out of phase. It is key to keep in mind that there is a spatial interpretation to these expressions; the total path each beam travels, as the device also travels, is longer than if the device was not moving. It is just that one of these longer paths is shorter than the other. Keeping up with these layers of interpretation will become important in this discussion. In fact, let’s look at what the spatial diagram looks to be.
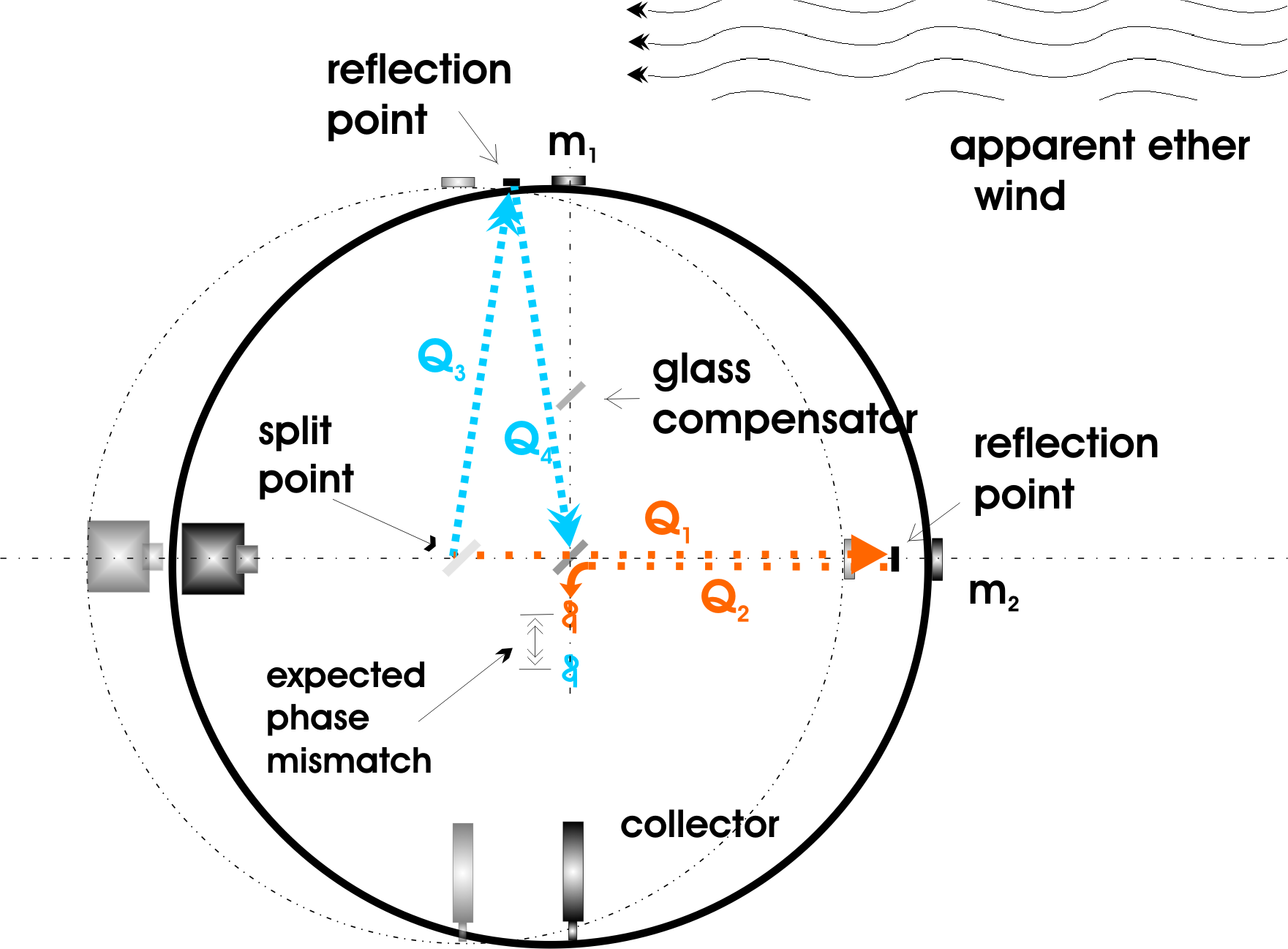
Sketch B
Here we see a reconstruction of the Michelson/ Morley interferometer. The original device was floated in mercury so that the apparent aether wind could be easily studied from any angle. Note Q1 and Q2, when summed, equal the total spatial path of the on-axis operation. Q3. and Q4, when summed, equal the total spatial path of the crossing operation. The analytical summary gives us this: The given expressions provide the individual times of the two spatial displacements that occur as the frame [Earth] moves through the same space that the light is moving through. This was the analytical construct of the Michelson/Morley interferometer experiment of 1887. Hopefully, one can see the dual nature of the argument. Q3. and Q4 show the inscribed vector path as the aether wind flows past the device. They also show the presumed spatial path of the beam from splitter to mirror and back to splitter when the frame is taken to move through space - in essence, the reciprocal of the flowing aether perspective. Taken together, we see a tidy bit of reversible math and logic in an applied setting. We will have comments on this construct later.
Seeing this spatial relief helps us see what Fitzgerald did two years later, acting as a theoretician and empirical tinker-er. Fitzgerald looked at the on-axis expression and realized that 2L/c/ 1- v2/c2 = 2L/c/ (sqrt(1- v2/c2)) (sqrt(1- v2/c2)) which is, in a purely mathematical sense, a root factor larger than 2L/c/ sqrt(1- v2/c2).
An easy way to make the longer time-cycle equal the shorter time-cycle would be to selectively shorten the Length to be traveled by the longer cycle. That shortening factor, namely, sqrt(1- v2/c2) does the job very handily. Now the time-cycle regulated by the normal expression 2L/c/ 1- v2/c2 is being applied to a shorter Length, and both time-cycles become equal => on-axis equals cross-axis.
More simply put , if you take one of the root factors of the on-axis expression and apply it to the physical quantity L, the net outcome gives you [2L/c/1- v2/c2 operating on L (sqrt(1- v2/c2))] to compare with
[2L/c/ sqrt(1- v2/c2 ) operating on L]. Now these cycle times will be equal, and, of course, the failure of the 1887experiment was that the beams emerged without any time lag between them, i.e., in-phase. So the Fitzgerald Contraction fixed the analytical expressions such that the expected outcome would match the real/observed outcome. This could be considered quite the empirical fix - just shorten one of the paths till the times are equal. ?.
And so, this is how things remained until Einstein grew up, and by 1905, could look at this original puzzle and solution - and then add his own nuances. Referring to the spatial reconstruction, he noticed that Q3 and Q4 required their own unique empirical recognition. They were saying, as it were, that time is inherently altered within the confines of such a frame. As the frame continues to move faster and faster, the time-cycles themselves, grow longer and longer - rooted, as it were, on the unchanging L of the cross axis. [For those properly aware, this is an observation still easily contained by classical mechanics…] And so, Einstein asserts - again, acting as theoretician and empirical tinker-er - since light is the absolute arbiter of information flow, the unit-time of any information flow is lengthening, ergo, time is slowing {dilating} for any such hi-velocity frame. And presto! Any outside observer can witness the slowing; any on-board observer is trapped by the information flow, itself, and cannot experience the slowing – all is normal to this hi-velocity passenger. And bonus to any such travelers, they age more slowly than any they left behind – younger brothers can become older brothers, and identical twins can come to diverge in age.
Einstein’s proposition expands thusly: You wake to find yourself floating at the center of a giant beach-ball, somewhere out in empty space. It is fairly clear that there is 20 feet in any direction to reach the inner wall. [Ball has 40 foot diameter.] As you gain your senses, you are unaware of any current acceleration, and more importantly, given your recent sleep time, you are unaware of any previous accelerations. You are in free-float, what Einstein will come to call relative rest. If you are moving at 0 km /sec, or 40 km /sec, from your position within the ball, you can never know it - meaning, prove it with some physical test within the sphere. In keeping with Einstein's model, the ball looks perfectly round from the inside – time is passing as you have always experienced it. Your situation is as normal as it has ever been. But someone outside the ball might see you to be passing them at an incredible rate, so fast, in fact, that your ball seems squeezed a bit flattish along your axis of travel. The shadows they see inside the ball reveal no movement, as if you are frozen still. From their scale of time, your scale of time is much longer. From their outside perspective, they can apply Einstein’s operators: T /sqrt(1- ov2/c2) and L (sqrt(1 – ov2/c2)) [ov => meant to represent Observed Velocity in observer’s scale; normally just called u ] to see exactly how your frame is altered by your observed velocity. Though they are tools that describe your situation, they are not in your arsenal of tools inside the sphere – you simply abide controlled by them. You are at relative rest.
Since 1905, there have come to pass observations that seem to support this model. But observations can often have another road to travel by.
*Take, for example, the very case that helped Michelson and Morley design their test. Michelson and Morley came along at the end of a period of serious inquiry into the nature of light. It was then well-understood that light had a very fast but finite velocity. But more telling for their case, it was well understood that light goes un-vectored by the source… You pilot a jet going 1000 mph. You approach a strip of desert that has two poles planted out in front of you; they are 100 yards apart. You flash a strobe briefly as you approach them. The poles have sensors that allow technicians tending them to measure the speed of the light-pulse as it moves through them. As you pass on well beyond the poles, you send another pulse, this time rearwards through them. The technicians again measure and, again, the light-pulse possesses the same speed. Your 1000 mph has no effect on the speed of the pulses; light acquires no addition velocity from the source.
Indeed, Michelson and Morley were relying heavily on the certitude of that observed fact; that light has a constant velocity through space. That being held true, it should be a rather predictive assertion that Earth’s velocity could be indexed against it. The 1887 interferometer was designed to do just that, but as we have seen in that last few pages, instead of it easily proving a set of conditions – the simple and rational extension of logic that the test represented hit the proverbial fan.
Einstein’s over-arching model of Special Relativity puts many things into a reasonable state, and supports thereof do exist. But just as Michelson and Morley were caught in unawares, is there a chance Einstein can be caught in unawares? We will begin to make that very case.
Despite the model of Special Relativity, it remains for us in our current relativistic frame (anywhere on Earth) to experience the nature of light. The little jet pilot still cannot make light go faster or less fast, and this can be dealt with, from his perspective, by Special Relativity. But, if we introduce another jet, things tend to go awry. Now one jet approaches the poles in the desert from the South, just as the other jet approaches them from the North. At nearly the same instant, both jets fire a pulse. The technicians will be a bit busier, but still they find that each pulse comes through at c. So far, so good, but since that time when Einstein’s model began to project its sway, Earth has been a relativistic frame. But note: from the instant each pulse crossed the center point between the poles, they began to separate at 2 light-seconds per second – a condition untenable in a relativistic frame. Some relief could come if we switch perspective to ride along with either pulse; then Einstein’s model is more rightly upheld. [Meaning, such a case is indefinable by default, and so, one light pulse can never assay the time /space relevance of another light pulse.] But the situation remains that the technicians live in a relativistic frame where an obvious violation of the model is revealed - the light pulses are clearly ripping past themselves at 2 light-seconds per second. The speed limit for items in a relativistic universe is 1 light-second per second; 2 light-seconds per second is out of gamut - perhaps not exactly for light pulses, but space craft separating from one another can never see the other exceeding 1c of separation. From here, must we make a more complex case? or can simplicity save the day. Suffice it to say that other violations exist for the discerning eye, but what new twist is called for? Maybe, just a fresh start.
Relying on the validity of the technicians plight, the 1887 interferometer can be re-visited. The key to a proper re-assessment is lying there in the desert scenario, if it can be properly prized away. At the instant the pulse is fired, a very real condition exists that is otherwise difficult to quantify in a lab setting – lab settings being the modern empirical standard. Newton could follow us here, one is hopeful about others. As the pulse leaves the strobe, the condition exists that finds the pulse and the source (jet) moving at two distinct velocities away from the point of emission – sadly, meaning a point in space. In a lab setting, a point in space is indefinable; meaning, not useful in the proper interrogation of natural phenomena. Yet this is the very experience the technicians must deal with in their relativistic frame. Somewhere left and right of the poles there are emission points above the desert floor where a jet and a pulse have left at their respective velocities. [For the moment, let’s not complicate matters with the fact that the desert floor is moving through space, as well.] If such an emission point in space could be held useful, we could find ourselves with powerful new terms. One of the most powerful terms, is the realization that the source does not impute any inertia to the mass-less entities that make up the pulse – light enters space at c; no physical additions due inertia- meaning Q3 and Q4 describe a null path . This idea impinges rather harshly on the design of the 1887 interferometer.
Reviewing Sketch A, we see P1 and M2 bounded by two arrows that insinuate the apparent aether wind. This, by default, sets up a vector scenario, where the device is fixed in the firmament [as Newton would have it]. And the two components, the apparent aether wind and the light beam, each have their requisite velocities, and in the first leg they work against each other and in the second leg they work with each other. It is notable that this is the primary interpretation taken-up in the 1887 design; it is the vector distillation of the spatial behavior - and technically, it is the analog of a moving-frame perspective/analysis. What is really happing is the frame is moving through the aether; Michelson/Morley relied on the reciprocal perspective of a moving wind.
Sketch A
As we approach what might be said to be really happening, we find ourselves facing a classic ground-figure problem. It is possible to utilize the same elements, and same math, but change the interpretive emphasis of the pieces in play. This time we ground the aether in the firmament, and have the device and the light beam be the components in motion, which comports better with the idea of Earth’s rotational and orbital underpinnings. True, the aether could still appear to be a wind, but we are not distracted; we are focusing on the reassertion of a simple Cartesian underpinning for this scenario. And interestingly, in this scenario you will need an emission point [origin on number line] fixed in the aether to show from where the device moved. Uniquely, the same math will satisfy both scenarios, and so, it is a quibble to favor one scenario over the other. But in so saying, we cleave much closer to what is actually happening - the moving-frame perspective overlain by the moving-wind perspective produces a perspective infarct. Each is virtually identical to the other, and yet wringing out each in its own light helps us see a little bit of wrong in each.
And so, when we look first at the on-axis analysis we see a perfect reciprocation of details; it is valid from either perspective, and it leaves us with little with which to be troubled. Alas, this charming congruence seems to anchor the total scenario too firmly.... For the on-axis compliment, both the moving-aether and the moving-frame scenarios, check-out okay; Michelson and Morley had this bit right. The same is not true for the cross-current, or perpendicular, compliment.
Sketch B
When we turn to the perpendicular compliment, Sketch B becomes helpful, but we must parse carefully. What we see literally is the moving-frame perspective overlain by the moving-wind perspective. Q3 and Q4 illustrate what the analytical expression sqrt(1- v2/c2 ) is depicting. Again, from the moving-wind perspective, we can say it is a vector assay; the light beam must buck the aether wind both there and back, requiring a longer time [path inscribed in the passing wind] for the operation than if there were no wind to buck. From the moving-frame perspective, Q3 and Q4 depict the light-path in spatial {Cartesian} terms that is analogous to the vector assay. Again, these reciprocals seem to fit nicely.
With the moving-wind/vector assay being held predominant, coming down to us from 1887, we see vector mechanics as vector mechanics, and not much gives. But if look closely at the moving-frame scenario, we might prize away a bit of carapace, and form ourselves a critique.
If we, indeed, fix the aether in the firmament and make only the device and the beam possess their respective components of motion, then we invariably face a discontinuity i.e. something is made more clear by seeing the frame as moving in the firmament of space. When we fire the beam across the moving device, the beam is not aware of any of this motion – it leaves the source un-vectored, and without any inertia. It travels a simple path grounded in the aether, and its inertia laws. It will move along the perpendicular without regard to the motion of the frame, or the vector analog written in by Michelson and Morley. See Sketch C
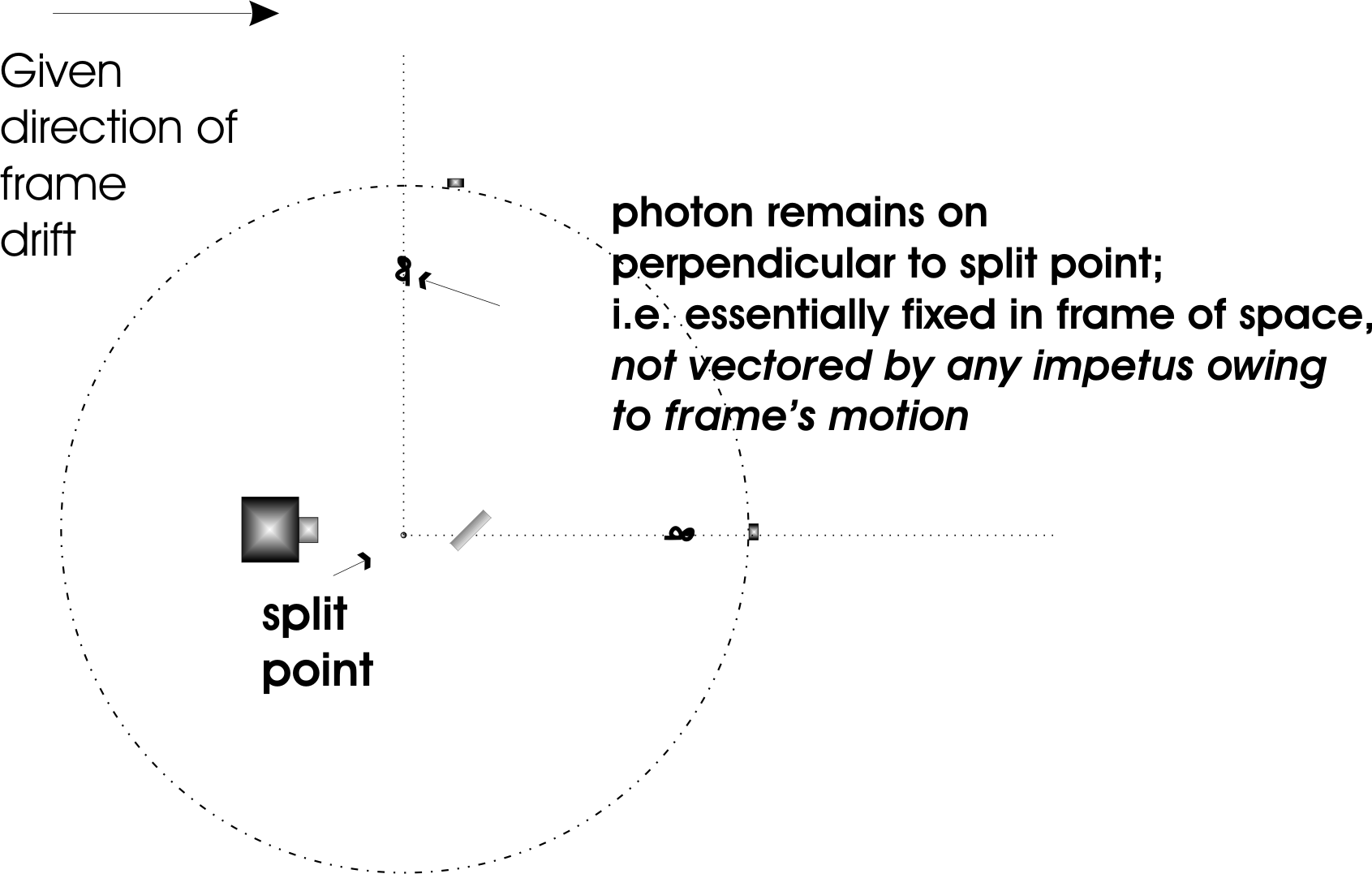Sketch C
Hopefully, it has been helpful to review what the moving-frame interpretation has to offer. When the frame moves in a grounded aether, light must obey rules that march it away from the expected path in the1887 design. But before we pursue this reasoning more carefully, there is a complexor that must be mentioned. See Sketch D
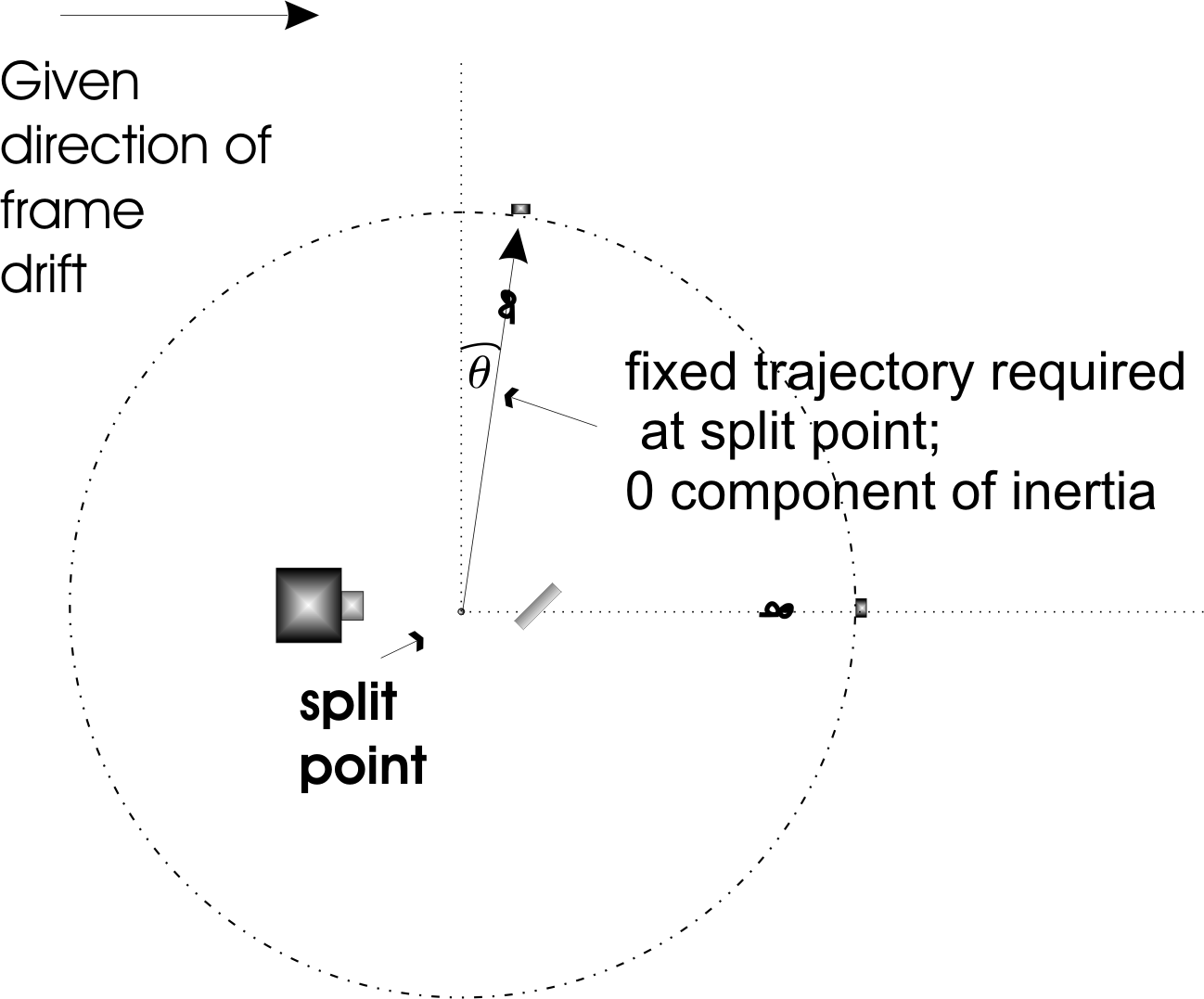Sketch D
It remains possible, in the moving-frame scenario/interpretation, for the beam to properly follow the prescribed path in the 1887 design. But it would require deflection at the splitter by that perfect angle to put it on the expected path (apparent vector). There would be no inertial component here, just a physical re-assignment for its path. There is no known mechanism to produce this deflection in this device, but it looms as a complexor that fortifies the original design.
[In Appendix 2, we will look more closely at these distinct abstracts. For now let's say the moving-aether is State 1, the moving-frame is State 2, the deflected path is State 3 and the zero-inertia path is State 4.]
Now our discussion tightens: when Einstein came upon the design elements of the 1887 interferometer – in light of the accepted Fitzgerald Contraction - his observations seemed prescient. But, we have just shown reasoning that makes suspect his prescient observations. If our arguments here are correct, then it is accurate to say that Einstein builds in a major flaw when he constructs Special Relativity – Einstein imputes inertia to a mass-less entity, de facto, by presuming it to follow a vector [ un-deflected spatial path represented by Q3 and Q4] it cannot - and this can be seen as a fatal flaw. What we are forced to say is the moving-wind perspective requires us to accept inertia in the beam to buck the wind and follow the implied vector path {State 1}, and perhaps more clearly, in the moving-frame perspective, inertia is required for the beam to launch itself down-range to follow the Q3 and Q4 spatial route {State 2} - and neither is permissible -- there is no inertia attributable to a mass-less entity.
Avi 1 shows us the presumed vector interpretation with respect to an apparent aether wind {State 1}. ref Sketch B
AVI 1
Note the inscribed V as it flows away with the aether. It is the life and death of Special Relativity.
Avi 2 shows us the aether as grounded and the frame in motion {State 2}. ref Sketch C
AVI 2
Though we can deduce by the tighter angles being inscribed in the aether that this is a slower moving frame, nonetheless, the 1887 {MMI} math is still perfectly intact.
Avi 3 shows us the complexor of a deflected beam {State 3}. ref Sketch D
AVI 3
The red-orange shadow depicts the ideal deflection angle for a given velocity and length, L.
AVI 4 {State 4}
Notice the blue sphere representing the origin in space; not welcome in a lab environment, all critical to understanding frames in motion through space
Understanding that AVI 1, 2, and 3 depict interpretations that can easily obscure one another, we must parse carefully. AVI 1 asks us to interpret the scenario from the point of view that holds the flow of the aether as dominant in the scheme – we see the apparent aether wind flowing past the general area of the device. This allows the device to be apparently fixed as the mass-less entity leaves the source, passes through the splitter and continues on to the mirror. Upon reflection the mass-less entity returns back to splitter, all inline with the apparently fixed source; more precisely, the point of divergence on the splitter. Michelson and Morley, therefore, saw the mass-less entity at war with, vectoring against, this aether wind. They used the math,
2L/c/ sqrt(1- v2/c2 ), to indicate this behavior. The reciprocal scheme {AVI 2} gives us the same outcome: if we change the dominant element to be an apparently moving device with respect to an apparently fixed aether, then the same math applies - if the mass-less entity is held to remain inline with the source through reflection and back. Of course, now we brave the observation that the mass-less entity cannot follow the mathematical prescription under either scheme.
However, AVI 3 shows us a correlate that is somewhat supportive of the base mathematical assertion maintained by Michelson and Morley, if we stay focused on the idea that the aether is fixed and the device is moving. If, at the splitter, the mass-less entity is deflected by just that amount that is correct for the L involved and the given velocity of the device, then the mass-less entity can appear to follow the vector proposition described by Michelson and Morley. The deflected mass-less entity will, in reality, remain inline with the source through reflection and return. This is possible because a mass-less entity can be deflected onto any new path in a fixed aether; it simply cannot carry the inherent inertia of the source. This is the grievous oversight built into the Michelson/Morley interferometer of 1887, and one can see it in the simple prescription of mathematics they assigned to the problem – which would be correct if the source could imbue a mas- less entity with inertia…
AVI 4 reveals to us what the proper construct of the scenario should be; specifically, the device is moving through a fixed aether and the mass-less entity goes unencumbered by inertia into a fixed aether. Interpreted as such, the mass-less entity follows a path inline with its emission point as the device moves, returning to a point on the splitter it did not pass through originally – and from that unique point it is reflected to find itself in-phase with the ray reflected along the line of motion. The Accommodation Sequence to follow will address the phase issue.
This assay clearly points to one correct interpretation – the waveforms should emerge in-phase; and this is the very outcome that did emerge from the first firing of the 1887 interferometer. They puzzled over this outcome because no one saw the incorrect imputation of inertia to a mass-less entity. Michelson and Morley did not see it; Fitzgerald did not see it; Einstein did not see it; who can un-see it now? We are left to point directly at the improper assignment of math in a very important physical test.
The puzzling outcome in 1887 results directly from misapplied mathematics; more precisely, a seemingly good model did not fit the problem at hand.
The corrected Accommodation Sequence follows…
If we follow the logic in Avi 4 we can make calculations…
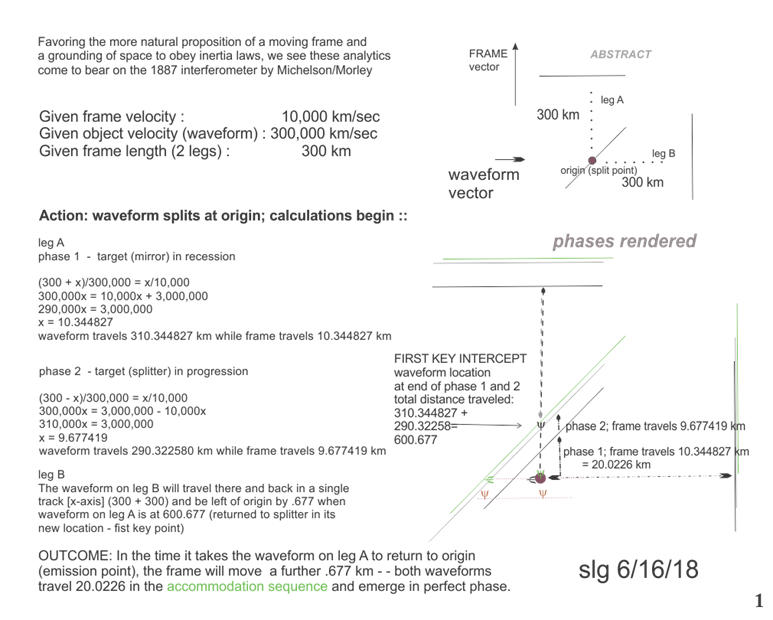
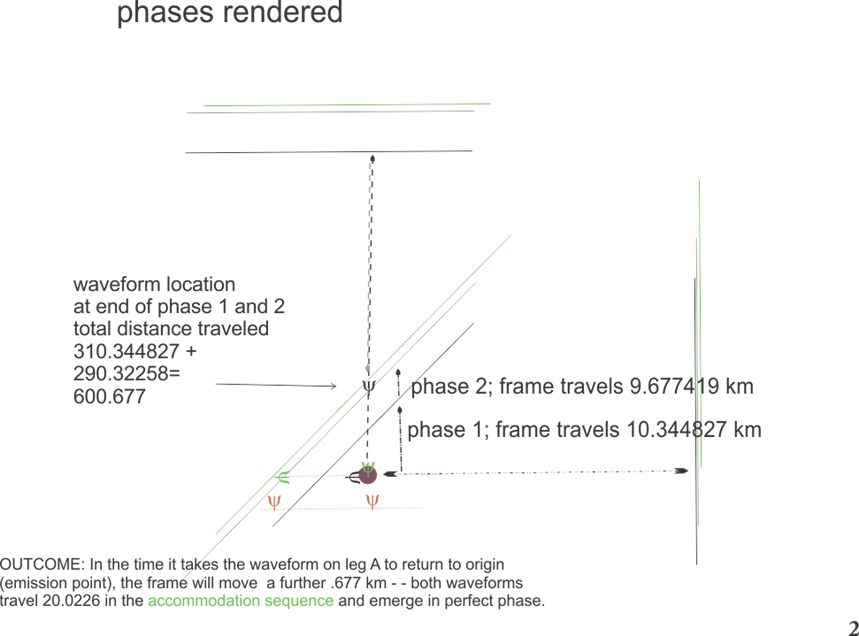
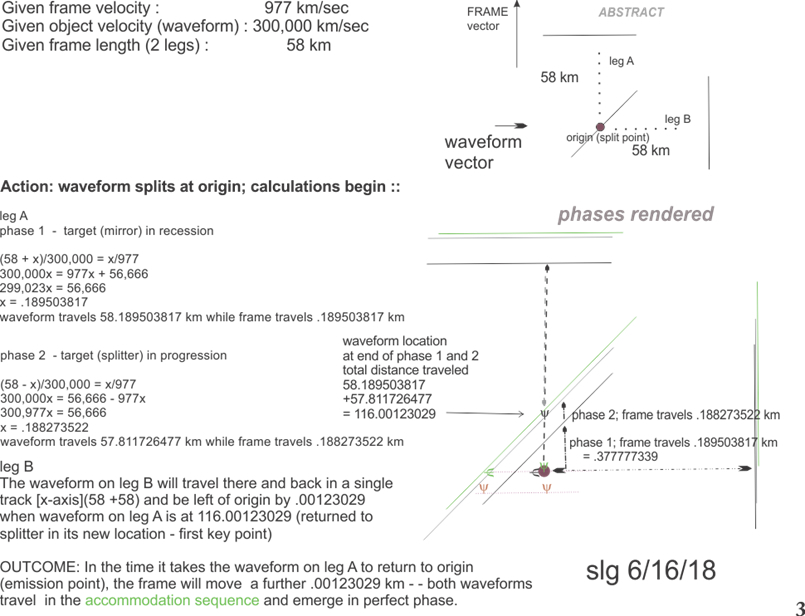
What the calculations bear out is that the 1887 interferometer is an harmonics trap. Without invoking Fitzgerald’s Contraction, and allowing the beam to obey inertia rules, the waveforms naturally fly out in-phase --as the physical device {MMI} proved in 1887. However, a gap does also appear, which belies the indexed {against light} motion of the frame -- it is merely delivered in the unexpected dimension.
Steven Louis Grillo 7/9/2018 best edit 8/27/2018
*Sketch A {Panels 4, 9 and 10}: Graphic taken from page 167, and clipped mathematics insert {Panel 16} taken from page 166, Gamow, George The Great Physicists from Galileo to Einstein, 1988 :: first published as Biography of Physics, 1961
Appendix 1
These observations beg us to review the original test and sift for a better way through. Sketch DD helps us re-acquire the elements.
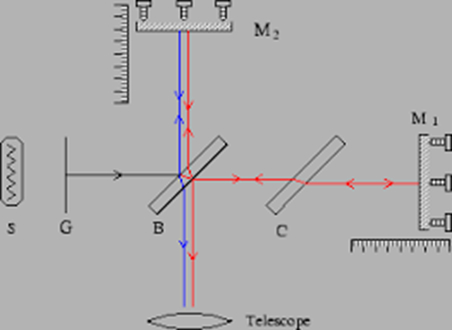Sketch DD
We call our attention the collecting telescope, here represented by the convex lens. Whereas it can be said that a convex lens could be useful in detecting beams separated in the vertical, it is exactly the wrong shape to collect separations in the horizontal; this is another reason why the truth we are promulgating here remains hidden. Sketch EE will help clarify.
Sketch EE
Note how the action of the lens draws beams together. This action, combined with the general diffusion of incoherent light, would significantly blend any gap between beams separated in the horizontal. Our logic, then, requires the opposite action, which we get with a concave lens. See Sketch FF.
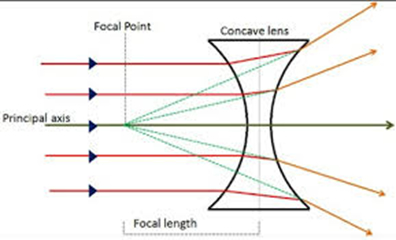Sketch FF
With a concave lens, we can see how a gap between beams in the horizontal can be exaggerated. Aided thusly, we can illustrate how the gap due the motion of Earth is in the horizontal plane, not the vertical plane. Anyone with open access to an M/M interferometer should seek to confirm these arguments with a simple fix as it applies to the collector. See Sketch GG.
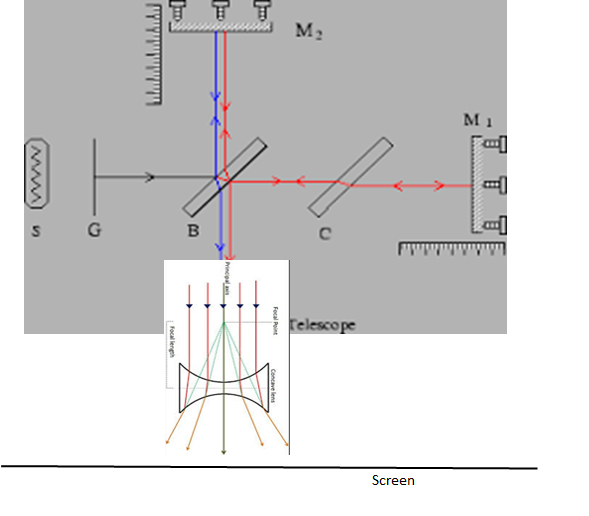Sketch GG
Those with the proper technical background will no doubt devise other exploitations.
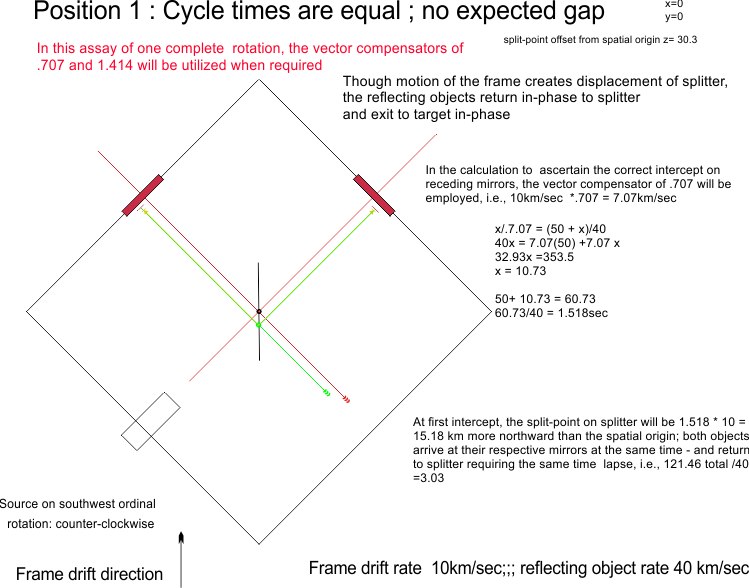
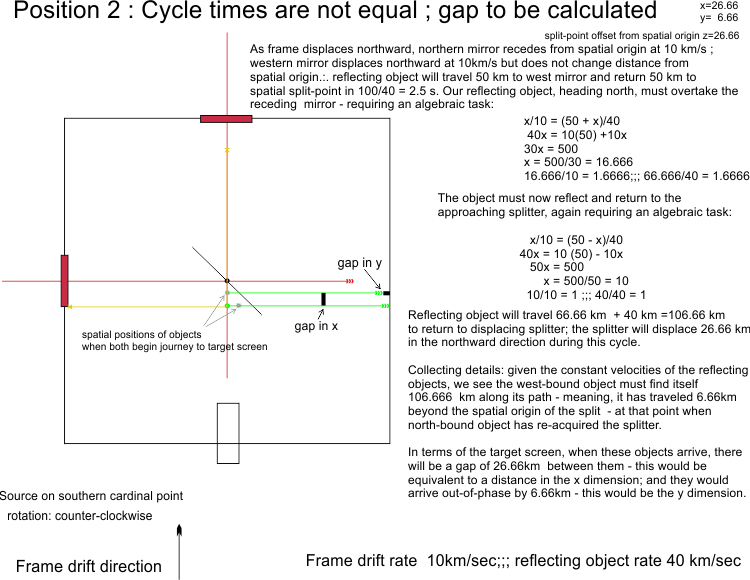
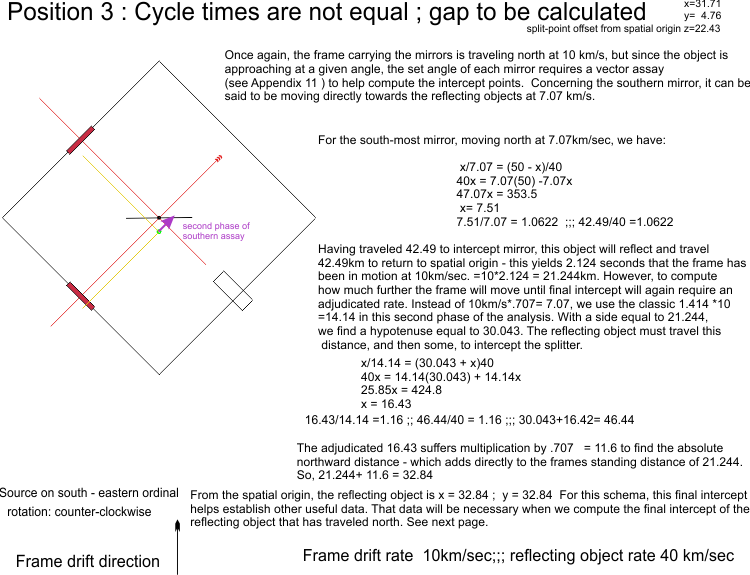
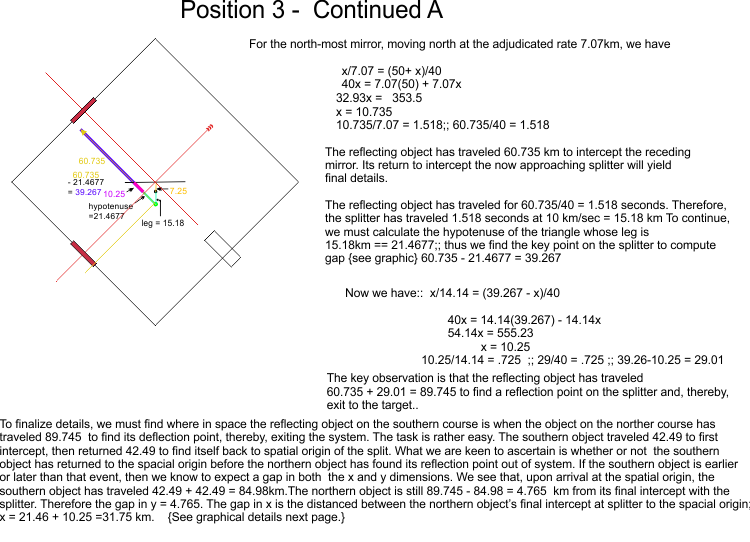
Extension *********************
To expand on the concave option, it occurs that all of the tuning of mirrors in standard interferometers violates the inherent need of the design. The two reflecting surfaces should be 90 degrees to one another. The accommodation sequence reveals that the gap due motion appears on the x-axis not the y-axis [which M/M expected]. The basic flaw in movable mirrors is that the gap is inherently tuned out of existence when the beams are aligned. [Even so there would be subtle noise appearing in the system as the beams shift during rotation, i.e., slight changes in luminosity.] So, for a device that would inform the validity of the Accommodation Sequence, the reflecting surfaces should be rigidly inscribed in an ingot by a hi-precision CNC machine lathe, and then grooved at 45 degrees to accept the splitter. If a thin enough laser beam is introduced into such a system the gap will appear due motion {of Earth} and then be sent to the target, where the concave lens is in the final path to broaden it accordingly. The panel below illustrates the design that would yield the results of a properly configured interferometer intended to integrate its motion with the frame of space and inertially neutral radiation.
The output would be, for one full rotation, two thin lines that separate and merge into one, 4 times each. [See Appendix 2]
Sketches DD, EE, and FF clipped from internet without attribution.
Appendix 2
*******************************************************
Appendix 3
Extension: The Four Analytical States of Concern; RE: Special Relativity Theory
Prologue: We will look closer at the four states of concern; those introduced elementally in the text proper [The Fundamental Assay]. This closer look will be supported by additional AVI files. Here we will review the dynamical material under discussion more succinctly, and offer re-proofing notes. States 1 and 2 are tightly linked analytically; they form an important ground-figure scenario, illustrating in State 1 the classic interpretation, and its reciprocal in State 2. State 3 depicts a conditional to State 2; it helps maintain a mathematical purity to States 1 and 2, but a caveat must be noted. State 4 presents an analytically clear, but historically un-noted scenario. When properly interpreted, it undermines the Fitzgerald Contraction and defines how Einstein’s model relies on the imputation of inertia to a mass-less entity. We must find this a fatal oversight for the Special Theory of Relativity. Moreover, the gap intended to reveal the motion of Earth presumed to appear in the 1887 Michelson/Morley interferometer does appear in State 4, though not as originally anticipated. Thus, Einstein’s postulate that no experiment within an inertially balanced frame will reveal its motion is rendered moot. Motion in any frame is readily detectable when the tenets of State 4 are recognized and the proper technical procedures are brought to bear.
State 1 AVI
In State 1 we see the classic MMI prospectus, where the aether wind is pre-dominant. In this we see the wind as the figure and the device as the ground. As the light pulse leaves the source, it travels to the splitter; from the splitter to the far mirror; and from the far mirror back to the splitter. The distance from the splitter to the far mirror is L; the cycle there and back for the pulse is therefore 2L. However the pulse must deal with the flow of aether, and the analytical procedure for that circumstance is depicted by the V inscribed in the flow-by of the aether. Though the calculation emphasizes the time lapse, the V we see inscribed in the aether is a real spatial track the pulse must be seen to follow at c. And this track is longer than 2L; hence we say the cycle-time along 2L for a moving frame is slower than for a frame that is not moving - and also, it is cycling slower than for a frame moving not so fast as it. Though we use the term moving frame in the last sentence, State 1 requires us to remain mindful of the argument that the frame is ground, and the aether wind is responsible for the inherent vector the pulse encounters.
For the observer riding along with the source, the cycle along 2L is all he can substantiate as a scientific truth; he is in no way privy to the inherently inscribed path the pulse has traveled in the aether wind. If the cycle-time along 2L is his on-board standard measure of time, then he will never know that his cycle is lagging behind a cycle on a non-moving frame. This, then, is the root of time dilation and the normalcy of relative rest. When the frame/device is taken as ground, the aether wind taken as figure forces a un-noticeable vector on the pulse, where the observer on-board holds the pulse to follow the perpendicular path from source to splitter, and continue along the perpendicular to cycle through 2L (to the far mirror and back to splitter). It is an un-noticeable vector except for the sentient who can see, mathematically, the impact of the aether wind. State 1, then, is the preferred historical interpretation. See Sketches A and B
Note: For the mathematically inclined, it is clear that the aether wind in State 1 AVI is a very fast moving wind.
State 2 AVI
In State 2 AVI we hold the aether as ground and the frame/device as the moving figure. Though the State 2 AVI depicts a slower moving frame, all of the essential elements remain conserved. If the observer were astride the source, he would observe the un-noticed vector keeping the pulse on the perpendicular to him as the frame moves. But clearly the aether remains fixed as the frame and pulse move through it. The same math works as perfectly for State 2 as it does for State 1. But we take note of the pink dot that represents the illustrated start point of the pulse; it remains fixed in the aether as the source (and observer) continues on.
But now we ask a critical question: If the pulse remains on the perpendicular to the observer in State 2 – as to comport with State 1 - how and why? For the pulse to follow the V in State 2, it must carry inertia from the source [more importantly, through the splitter] – and this is not possible. Mass-less entities cannot carry inertia; and so, the un-noticed vector in State 1 and State 2 is impossible. Or is it?
State 3 AVI
State 3 AVI depicts State 2 AVI exactly. However, we allow ourselves a given: we presume the pulse to be deflected at the splitter by exactly the amount that would have it follow the inscribed V in the aether{ red-orange shadow }. It remains conclusive that a mass-less entity can be reflected or deflected along any path open to it, requiring nothing of the concept of inertia. A perfect deflection angle would allow the pulse to follow the inscribed V without violations of any sort. This mathematically solid argument helps certify the general conditions proffered in States 1 and 2. However, there is no known mechanism to physically produce this deflection in the MMI. Though the most analytically clean scenario, it fails in practice to help redeem States 1 and 2.
Keep in mind that States 1, 2 and 3 all exist here to help support the original Michelson/Morley analytical procedures, whereby the pulse, in following the perpendicular path, takes less time to return to the splitter than the pulse that was split off to follow the on-axis path. The proposed mismatch in the cycle-times was presumed to be due to Earth’s fundamental motion. When no mismatch (expected fringing) was found, it was left as a puzzle in physics until Fitzgerald produced a conjectural solution involving a shrinkage of L along the axis of motion – by just that amount that creates equal cycle-times for the independent pulses [on-axis and cross-axis]. However, there is no known mechanism to account for this shrinkage, except for the conjecture itself. But it stuck. And it was made all the sweeter when Einstein incorporated it into his own empirical observation. This observation held that the slowed cycle-times we witnessed in States 1,2 and 3, working in conjunction with the Fitzgerald shrinkage, suggested that such a frame is in a wholly unique expression of existence. The very physics of the frame were held in thrall to this slowed cycle, such that the given frame, in toto, had its own relationship to time – things age slower there. And beauty of beauties, the observer on-board would never know it – all would seem normal to him. And there would be no test he could ever perform that would reveal his inherent motion.
State 4 AVI
Dutifully, we turn to State 4 AVI, where we find the aether as ground and the moving frame as figure, and witness what nature would provide – an emission of a pulse that possess no inertia. The pulse is orphaned at the emission point and travels a path without heed to the moving away of the source and observer. It passes through the splitter at one point and returns to intercept the splitter at a different point. The implications here are profound. As the Accommodation Sequence in the text proper reveals, the pulses following this state of affairs sees the pulses emerging from the splitter perfectly in-phase, but with a gap between them owing to the motion of the frame.
Michelson and Morley expected the gap to be on the axis of motion, where State 4 reveals the gap to be on the cross-axis. There is no need to invoke the Fitzgerald shrinkage and, whereas the cycle-times do increase with velocity, the illusion of Relative Rest is broken because the gap can easily be garnered with the proper technical procedures – on any moving frame… Sentient beings should know they are moving through space when that is their future enterprise. State 4 clears the way.
The following AVI file depicts the Accommodation Sequence in close detail. We see the pulses in-phase and the gap indexed to the velocity of the frame. {The animation package at hand makes it difficult to synchronize all photon behaviors perfectly. Though stuttering, the phased depictions are in accord with the math algorithms constituting the Accommodation Sequence.}
Final comparison: Michelson/Morley vs Accommodation Sequence
On the left we see the output of the Accommodation Sequence, on the right we see the expectation of Michelson and Morley under a State 2 {moving frame} perspective, or to provide the correction they would need, a State 3 perspective {deflection at splitter}.
Historical Addendum: The Pulsar exam
By early 2008, I had become convinced that there was a bug in Special Relativty. Notwithstanding the fact that in 1990 I had designed a test that seemd perfectly valid as a completion of Michelson's effort, i.e., to index the motion of Earth against the constant spatail velocity of light; I knew there was a correction to be made somewhere in the provenance of the SR model. The test I designed seemed to easily violate the tenets of Relative Rest, but in itself did not offer or point to a root correction. On this website, all of the argumentaion found above is what I consider to be that correction. But of course that insight did not occur until 2018. Back in 2008 I wrote the Pulsar Exam to elucidate my take on the issues that seemed wanting a clearer development. The essential assay found in the Pulsar Exam was intended to help validate the reasaoning that the 1990 test relied upon. I find the Pulsar Exam to be a very good primer for those that find curiosities in the Special Relativity Theory. And a very good run-up to Michelson's Error. SLG 8/22
See Pulsar Exam